Comprimento de onda
Em meios lineares, qualquer padrão de onda pode ser descrito em termos da propagação independente dos componentes sinusoidais. O comprimento de onda λ de uma forma de onda sinusoidal viajando a velocidade constante v é dado por
λ = v f , {\\i1}lambda ={\i}frac {\i},{\i},{\i},div>
onde v é chamada a velocidade de fase (magnitude da velocidade de fase) da onda e f é a frequência da onda. Num meio dispersivo, a própria velocidade de fase depende da frequência da onda, tornando a relação entre o comprimento de onda e a frequência não linear.
No caso da radiação electromagnética – como a luz no espaço livre, a velocidade de fase é a velocidade da luz, cerca de 3×108 m/s. Assim, o comprimento de onda de uma onda eletromagnética (rádio) de 100 MHz é aproximadamente: 3×108 m/s dividido por 108 Hz = 3 metros. O comprimento de onda da luz visível varia de vermelho profundo, cerca de 700 nm, a violeta, cerca de 400 nm (para outros exemplos, ver espectro electromagnético).
Para ondas sonoras no ar, a velocidade do som é de 343 m/s (à temperatura ambiente e à pressão atmosférica). Os comprimentos de onda das frequências sonoras audíveis para o ouvido humano (20 Hz-20 kHz) estão assim entre aproximadamente 17 m e 17 mm, respectivamente. Frequências um pouco mais altas são usadas pelos morcegos para que eles possam resolver alvos menores que 17 mm. Os comprimentos de onda no som audível são muito maiores do que os da luz visível.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Por exemplo, para uma onda electromagnética, se a caixa tem paredes metálicas ideais, a condição para nós nas paredes resulta porque as paredes metálicas não podem suportar um campo eléctrico tangencial, forçando a onda a ter amplitude zero na parede.
A onda estacionária pode ser vista como a soma de duas ondas sinusoidais viajantes de velocidades opostas. Consequentemente, comprimento de onda, período e velocidade de onda estão relacionados, tal como para uma onda viajante. Por exemplo, a velocidade da luz pode ser determinada a partir da observação de ondas em pé numa caixa metálica contendo um vácuo ideal.
Representação matemáticaEditar
Ondas sinusoidais viajantes são frequentemente representadas matematicamente em termos da sua velocidade v (na direcção x), frequência f e comprimento de onda λ as:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ) estilo de jogo y(x,t)=Acos esquerda(2)(x-vt)|-esquerda(2)(x-vt)|-esquerda(x)(x-vt)|-direita)=Acos esquerda(2)(x-vt)|-esquerda(x-vt)|-direita)=Acos esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x-vt)|-esquerda(x)\ t)=Acos esquerda(2)(x-vt)|-esquerda(2)(x-vt)|-esquerda(2)(x-vt)|-direita)=Acos esquerda(2)(x-vt)|direita)p> onde y é o valor da onda em qualquer posição x e tempo t, e A é a amplitude da onda. Eles também são comumente expressos em termos de número de onda k (2π vezes o recíproco de comprimento de onda) e frequência angular ω (2π vezes a frequência) as: y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\\i1}displaystyle y(x,{\i)=A{\i1}cos {\i1}esquerda(kx-omega t{\i}direita)=A{\i(k(x-vt){\i}

em que comprimento de onda e número de onda estão relacionados com a velocidade e frequência como:
k = 2 π λ = 2 π f v = ω v , {\i1}displaystyle k={\i}{\i}{\i}={\i1}frac {\i}={\i frac {\i f}{\i}={\i1}frac {\i}{\i}{\i1}

ou
λ = 2 π k = 2 π v ω = v f . lambda =frac {2}{k}={2}frac {2}pi v}{2}{2}pi v}{mega }={v}frac {v}.{v}
 lambda ={\i1}frac {\i}{\i}{\i1}frac {\i}{\i1}}{\i1}}frac {\i}{\i1}}{\i1}}”>
lambda ={\i1}frac {\i}{\i}{\i1}frac {\i}{\i1}}{\i1}}frac {\i}{\i1}}{\i1}}”>Na segunda forma dada acima, a fase (kx – ωt) é frequentemente generalizada para (k-r – ωt), substituindo o ondenumber k por um vector de onda que especifica a direcção e o ondenumber de uma onda plana no espaço 3, parametrizado pelo vector de posição r. Nesse caso, o número de onda k, a magnitude de k, ainda está na mesma relação com o comprimento de onda como mostrado acima, sendo v interpretado como velocidade escalar na direção do vetor de onda. A primeira forma, usando comprimento de onda recíproco na fase, não generaliza tão facilmente para uma onda numa direção arbitrária.
Generalizações para sinusoidais de outras fases, e para exponenciais complexos, também são comuns; veja onda plana. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. Em particular, a velocidade da luz em um meio é menor do que no vácuo, o que significa que a mesma freqüência corresponderá a um comprimento de onda menor no meio do que no vácuo, como mostra a figura à direita.
Esta mudança na velocidade ao entrar em um meio causa refração, ou uma mudança na direção das ondas que encontram a interface entre os meios em um ângulo. Para ondas eletromagnéticas, essa mudança no ângulo de propagação é governada pela lei de Snell.
A velocidade da onda em um meio não só pode diferir da velocidade em outro, mas a velocidade tipicamente varia com o comprimento de onda. Como resultado, a mudança de direção ao entrar em um meio diferente muda com o comprimento de onda da onda.
Para ondas electromagnéticas a velocidade num meio é governada pelo seu índice de refracção de acordo com
v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})},}

onde c é a velocidade da luz no vácuo e n(λ0) é o índice de refração do meio no comprimento de onda λ0, onde este último é medido no vácuo e não no meio. O comprimento de onda correspondente no meio é
λ = λ 0 n ( λ 0 ) . lambda = lambda _{0}}{n(lambda _0}}}.}{n(lambda _{0}}}.}

Quando os comprimentos de onda da radiação electromagnética são citados, o comprimento de onda no vácuo normalmente é pretendido, a menos que o comprimento de onda seja especificamente identificado como o comprimento de onda em algum outro meio. Na acústica, onde um meio é essencial para que as ondas existam, o valor do comprimento de onda é dado para um meio especificado.
A variação da velocidade da luz com o comprimento de onda é conhecida como dispersão, e também é responsável pelo fenômeno familiar no qual a luz é separada em cores componentes por um prisma. A separação ocorre quando o índice de refração dentro do prisma varia com o comprimento de onda, assim comprimentos de onda diferentes se propagam em diferentes velocidades dentro do prisma, fazendo com que eles se refractem em diferentes ângulos. A relação matemática que descreve como a velocidade da luz dentro de um meio varia com o comprimento de onda é conhecida como relação de dispersão.
Meio não uniformeEdit

Comprimento de onda pode ser um conceito útil mesmo que a onda não seja periódica no espaço. Por exemplo, numa onda oceânica que se aproxima da costa, mostrada na figura, a onda de entrada ondula com um comprimento de onda local variável que depende em parte da profundidade do fundo do mar, em comparação com a altura da onda. A análise da onda pode ser baseada na comparação do comprimento de onda local com a profundidade da água local.

Ondas que são sinusoidais no tempo mas se propagam através de um meio cujas propriedades variam com a posição (um meio não homogêneo) podem se propagar a uma velocidade que varia com a posição, e como resultado podem não ser sinusoidais no espaço. A figura à direita mostra um exemplo. À medida que a onda abranda, o comprimento de onda diminui e a amplitude aumenta; após um local de resposta máxima, o comprimento de onda curto está associado a uma perda elevada e a onda morre.
A análise das equações diferenciais de tais sistemas é frequentemente feita aproximadamente, usando o método WKB (também conhecido como o método Liouville-Green). O método integra fase através do espaço utilizando um número de onda local, que pode ser interpretado como indicando um “comprimento de onda local” da solução em função do tempo e do espaço. Este método trata o sistema localmente como se fosse uniforme com as propriedades locais; em particular, a velocidade de onda local associada a uma frequência é a única coisa necessária para estimar o número de onda ou comprimento de onda local correspondente. Além disso, o método calcula uma amplitude que muda lentamente para satisfazer outras restrições das equações ou do sistema físico, tais como para a conservação de energia na onda.
CrystalsEdit
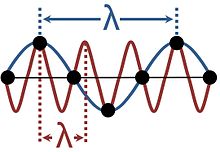
Ondas em sólidos cristalinos não são contínuas, pois são compostas por vibrações de partículas discretas dispostas em uma malha regular. Isto produz aliasing porque a mesma vibração pode ser considerada como tendo uma variedade de comprimentos de onda diferentes, como mostrado na figura. Descrições usando mais de um desses comprimentos de onda são redundantes; é convencional escolher o comprimento de onda mais longo que se encaixa no fenômeno. O intervalo de comprimentos de onda suficiente para fornecer uma descrição de todas as ondas possíveis em um meio cristalino corresponde aos vetores de onda confinados à zona Brillouin.
Esta indeterminação no comprimento de onda em sólidos é importante na análise de fenômenos de ondas como bandas de energia e vibrações de treliça. Ela é matematicamente equivalente ao aliasing de um sinal que é amostrado em intervalos discretos.
