Lungime de undă

Undele staționare sinusoidale într-o cutie care constrânge punctele de capăt să fie noduri vor avea un număr întreg de jumătăți de undă care se potrivesc în cutie.

A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue)

Standing wavesEdit

A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.

The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. De exemplu, pentru o undă electromagnetică, dacă cutia are pereți metalici ideali, condiția pentru noduri la pereți rezultă deoarece pereții metalici nu pot suporta un câmp electric tangențial, forțând unda să aibă amplitudine zero la perete.

Unda staționară poate fi privită ca suma a două unde sinusoidale care se deplasează cu viteze orientate opus. În consecință, lungimea de undă, perioada și viteza undei sunt legate la fel ca în cazul unei unde călătoare. De exemplu, viteza luminii poate fi determinată din observarea undelor staționare într-o cutie metalică ce conține un vid ideal.

Reprezentare matematicăEdit

Undele sinusoidale călătoare sunt adesea reprezentate matematic în funcție de viteza lor v (în direcția x), frecvența f și lungimea de undă λ ca:

y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

unde y este valoarea undei în orice poziție x și timp t, iar A este amplitudinea undei. Ele sunt, de asemenea, exprimate în mod obișnuit în termeni de număr de undă k (de 2π ori reciproca lungimii de undă) și de frecvență unghiulară ω (de 2π ori frecvența) ca:

y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\dreapta)=A\cos \left(k(x-vt)\dreapta)}

în care lungimea de undă și numărul de undă sunt legate de viteză și frecvență astfel:

k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}

sau

λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}

În cea de-a doua formă dată mai sus, faza (kx – ωt) este adesea generalizată în (k-r – ωt), prin înlocuirea numărului de undă k cu un vector de undă care specifică direcția și numărul de undă al unei unde plane în spațiul 3, parametrizat de vectorul de poziție r. În acest caz, numărul de undă k, mărimea lui k, se află în continuare în aceeași relație cu lungimea de undă, așa cum s-a arătat mai sus, v fiind interpretat ca viteză scalară în direcția vectorului de undă. Prima formă, folosind lungimea de undă reciprocă în fază, nu se generalizează la fel de ușor la o undă într-o direcție arbitrară.

Generalizările la sinusoide cu alte faze și la exponențiale complexe sunt, de asemenea, comune; vezi undă plană. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave

A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit

Wavelength is decreased in a medium with slower propagation.

Refraction: upon entering a medium where its speed is lower, the wave changes direction.

Separation of colors by a prism (click for animation)

The speed of a wave depends upon the medium in which it propagates. În special, viteza luminii într-un mediu este mai mică decât în vid, ceea ce înseamnă că aceeași frecvență va corespunde unei lungimi de undă mai scurte în mediu decât în vid, așa cum se arată în figura din dreapta.

Această modificare a vitezei la intrarea într-un mediu determină refracția sau schimbarea direcției undelor care întâlnesc interfața dintre medii sub un anumit unghi. Pentru undele electromagnetice, această modificare a unghiului de propagare este guvernată de legea lui Snell.

Viteza undelor într-un mediu nu numai că poate fi diferită de cea din alt mediu, dar viteza variază de obicei cu lungimea de undă. Ca urmare, schimbarea de direcție la intrarea într-un mediu diferit se modifică odată cu lungimea de undă a undei.

Pentru undele electromagnetice, viteza într-un mediu este guvernată de indicele de refracție al acestuia conform

v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

unde c este viteza luminii în vid și n(λ0) este indicele de refracție al mediului la lungimea de undă λ0, unde acesta din urmă este măsurat în vid și nu în mediu. Lungimea de undă corespunzătoare în mediu este

λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}}{n(\lambda _{0})}}.}.

Când sunt citate lungimi de undă ale radiației electromagnetice, de obicei se înțelege lungimea de undă în vid, cu excepția cazului în care lungimea de undă este identificată în mod specific ca fiind lungimea de undă într-un alt mediu. În acustică, unde un mediu este esențial pentru ca undele să existe, valoarea lungimii de undă este dată pentru un mediu specificat.

Variația vitezei luminii cu lungimea de undă este cunoscută sub numele de dispersie și este, de asemenea, responsabilă pentru fenomenul familiar în care lumina este separată în culori componente de către o prismă. Separarea apare atunci când indicele de refracție din interiorul prismei variază cu lungimea de undă, astfel încât diferite lungimi de undă se propagă cu viteze diferite în interiorul prismei, ceea ce face ca acestea să se refracteze la unghiuri diferite. Relația matematică care descrie modul în care viteza luminii într-un mediu variază în funcție de lungimea de undă este cunoscută sub numele de relație de dispersie.

Mediile neuniformeEdit

Diferite lungimi de undă locale de la creastă la creastă într-un val oceanic care se apropie de țărm

Lungimea de undă poate fi un concept util chiar dacă valul nu este periodic în spațiu. De exemplu, într-un val oceanic care se apropie de țărm, prezentat în figură, valul de intrare ondulează cu o lungime de undă locală variabilă care depinde în parte de adâncimea fundului mării în comparație cu înălțimea valului. Analiza valului se poate baza pe compararea lungimii de undă locale cu adâncimea locală a apei.

Unda sinusoidală care se deplasează într-un mediu neuniform, cu pierderi

Undele care sunt sinusoidale în timp, dar care se propagă printr-un mediu ale cărui proprietăți variază în funcție de poziție (un mediu neomogen) se pot propaga cu o viteză care variază în funcție de poziție și, ca urmare, pot să nu fie sinusoidale în spațiu. Figura din dreapta prezintă un exemplu. Pe măsură ce unda încetinește, lungimea de undă devine mai scurtă și amplitudinea crește; după un loc de răspuns maxim, lungimea de undă scurtă este asociată cu o pierdere mare și unda se stinge.

Analiza ecuațiilor diferențiale ale unor astfel de sisteme se face adesea în mod aproximativ, folosind metoda WKB (cunoscută și sub numele de metoda Liouville-Green). Metoda integrează faza prin spațiu folosind un număr de undă local, care poate fi interpretat ca indicând o „lungime de undă locală” a soluției în funcție de timp și spațiu. această metodă tratează sistemul la nivel local ca și cum ar fi uniform cu proprietățile locale; în special, viteza locală a undei asociată cu o frecvență este singurul lucru necesar pentru a estima numărul de undă local corespunzător sau lungimea de undă. În plus, metoda calculează o amplitudine care se modifică lent pentru a satisface alte constrângeri ale ecuațiilor sau ale sistemului fizic, cum ar fi pentru conservarea energiei în undă.

CrystalsEdit

O undă pe o linie de atomi poate fi interpretată în funcție de o varietate de lungimi de undă.

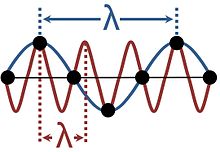
Undele în solidele cristaline nu sunt continue, deoarece sunt compuse din vibrații ale unor particule discrete dispuse într-o rețea regulată. Acest lucru produce aliasing, deoarece aceeași vibrație poate fi considerată ca având o varietate de lungimi de undă diferite, așa cum se arată în figură. Descrierile care utilizează mai mult de una dintre aceste lungimi de undă sunt redundante; este convențional să se aleagă cea mai lungă lungime de undă care se potrivește fenomenului. Gama de lungimi de undă suficientă pentru a oferi o descriere a tuturor undelor posibile într-un mediu cristalin corespunde vectorilor de undă confinați în zona Brillouin.

Această indeterminare a lungimii de undă în solide este importantă în analiza fenomenelor ondulatorii, cum ar fi benzile de energie și vibrațiile rețelei. Ea este echivalentă din punct de vedere matematic cu aliasing-ul unui semnal care este eșantionat la intervale discrete.

.